Title: 九大排序算法 · Issue #165 · sisterAn/JavaScript-Algorithms · GitHub
Open Graph Title: 九大排序算法 · Issue #165 · sisterAn/JavaScript-Algorithms
X Title: 九大排序算法 · Issue #165 · sisterAn/JavaScript-Algorithms
Description: 14.1 冒泡排序 原理: 从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。 动图演示: 代码实现: function bubbleSort(arr) { for (let i = 0; i < arr.length; i++) { for (let j = 0; j < arr.length - i - 1; j++) { if (arr[j] > arr[...
Open Graph Description: 14.1 冒泡排序 原理: 从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。 动图演示: 代码实现: function bubbleSort(arr) { for (let i = 0; i < arr.length; i++) { for (let j = 0; j < arr....
X Description: 14.1 冒泡排序 原理: 从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。 动图演示: 代码实现: function bubbleSort(arr) { for (let i = 0; i < arr.length; i++) { for (let j = 0; j <...
Opengraph URL: https://github.com/sisterAn/JavaScript-Algorithms/issues/165
X: @github
Domain: patch-diff.githubusercontent.com
{"@context":"https://schema.org","@type":"DiscussionForumPosting","headline":" 九大排序算法","articleBody":"\r\n\r\n## 14.1 冒泡排序\r\n\r\n**原理:**\r\n\r\n从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。\r\n\r\n**动图演示:**\r\n\r\n\r\n\r\n**代码实现:**\r\n\r\n```js\r\nfunction bubbleSort(arr) {\r\n for (let i = 0; i \u003c arr.length; i++) {\r\n for (let j = 0; j \u003c arr.length - i - 1; j++) {\r\n if (arr[j] \u003e arr[j + 1]) {\r\n const temp = arr[j];\r\n arr[j] = arr[j + 1];\r\n arr[j + 1] = temp;\r\n }\r\n }\r\n }\r\n}\r\n\r\n// 改进冒泡排序\r\nfunction bubbleSort1(arr) {\r\n for (let i = 0; i \u003c arr.length; i++) {\r\n // 提前退出冒泡循环的标识位\r\n let flag = false;\r\n for (let j = 0; j \u003c arr.length - i - 1; j++) {\r\n if (arr[j] \u003e arr[j + 1]) {\r\n const temp = arr[j];\r\n arr[j] = arr[j + 1];\r\n arr[j + 1] = temp;\r\n flag = true;\r\n // 表示发生了数据交换\r\n }\r\n }\r\n // 没有数据交换\r\n if(!flag) break\r\n }\r\n}\r\n\r\n\r\n// 测试\r\nlet arr = [1, 3, 2, 5, 4]\r\nbubbleSort(arr)\r\nconsole.log(arr) // [1, 2, 3, 4, 5]\r\n\r\nlet arr1 = [1, 3, 2, 5, 4]\r\nbubbleSort1(arr1)\r\nconsole.log(arr1) // [1, 2, 3, 4, 5]\r\n```\r\n\r\n**复杂度分析:**\r\n\r\n- 时间复杂度: 最好时间复杂度 O(n),平均时间复杂度 O(n^2^)\r\n- 空间复杂度:O(1)\r\n\r\n## 14.2 选择排序\r\n\r\n**原理**\r\n\r\n从未排序的序列中找到最大(或最小的)放在已排序序列的末尾(为空则放在起始位置),重复该操作,知道所有数据都已放入已排序序列中。\r\n\r\n**动态演示**\r\n\r\n\r\n\r\n**代码实现**\r\n\r\n```js\r\nfunction selectionSort(arr) {\r\n let length = arr.length,\r\n indexMin\r\n for(let i = 0; i \u003c length - 1; i++) {\r\n indexMin = i\r\n for(let j = i; j \u003c length; j++) {\r\n if(arr[indexMin] \u003e arr[j]) {\r\n indexMin = j\r\n }\r\n }\r\n if(i !== indexMin) {\r\n let temp = arr[i]\r\n arr[i] = arr[indexMin]\r\n arr[indexMin] = temp\r\n }\r\n }\r\n}\r\n\r\n// 测试\r\nlet arr = [1, 3, 2, 5, 4]\r\nselectionSort(arr)\r\nconsole.log(arr) // [1, 2, 3, 4, 5]\r\n```\r\n\r\n**复杂度分析**\r\n\r\n**时间复杂度:**O(n^2^)\r\n\r\n**空间复杂度:**O(1)\r\n\r\n## 14.3 归并排序\r\n\r\n**原理**\r\n\r\n它采用了分治策略,将数组分成2个较小的数组,然后每个数组再分成两个更小的数组,直至每个数组里只包含一个元素,然后将小数组不断的合并成较大的数组,直至只剩下一个数组,就是排序完成后的数组序列。\r\n\r\n实现步骤:\r\n\r\n- 将原始序列平分成两个小数组\r\n- 判断小数组长度是否为1,不为1则继续分裂\r\n- 原始数组被分称了长度为1的多个小数组,然后合并相邻小数组(有序合并)\r\n- 不断合并小数组,直到合并称一个数组,则为排序后的数组序列\r\n\r\n**动图演示**\r\n\r\n\r\n\r\n**代码实现**\r\n\r\n```js\r\nfunction mergeSort(arr) {\r\n let array = mergeSortRec(arr)\r\n return array\r\n}\r\n\r\n// 若分裂后的两个数组长度不为 1,则继续分裂\r\n// 直到分裂后的数组长度都为 1,\r\n// 然后合并小数组\r\nfunction mergeSortRec(arr) {\r\n let length = arr.length\r\n if(length === 1) {\r\n return arr\r\n }\r\n let mid = Math.floor(length / 2),\r\n left = arr.slice(0, mid),\r\n right = arr.slice(mid, length)\r\n return merge(mergeSortRec(left), mergeSortRec(right))\r\n}\r\n\r\n// 顺序合并两个小数组left、right 到 result\r\nfunction merge(left, right) {\r\n let result = [],\r\n ileft = 0,\r\n iright = 0\r\n while(ileft \u003c left.length \u0026\u0026 iright \u003c right.length) {\r\n if(left[ileft] \u003c right[iright]){\r\n result.push(left[ileft ++])\r\n } else {\r\n result.push(right[iright ++])\r\n }\r\n }\r\n while(ileft \u003c left.length) {\r\n result.push(left[ileft ++])\r\n }\r\n while(iright \u003c right.length) {\r\n result.push(right[iright ++])\r\n }\r\n return result\r\n}\r\n\r\n// 测试\r\nlet arr = [1, 3, 2, 5, 4]\r\nconsole.log(mergeSort(arr)) // [1, 2, 3, 4, 5]\r\n```\r\n\r\n**复杂度分析**\r\n\r\n**时间复杂度:**O(nlog~2~n)\r\n\r\n**空间复杂度:**O(n)\r\n\r\n## 14.4 快速排序\r\n\r\n**原理**\r\n\r\n和归并排序一致,它也使用了分治策略的思想,它也将数组分成一个个小数组,但与归并不同的是,它实际上并没有将它们分隔开。\r\n\r\n快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。\r\n\r\n快排的过程简单的说只有三步:\r\n\r\n- 首先从序列中选取一个数作为基准数\r\n- 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 `partition`)\r\n- 然后分别对基准的左右两边重复以上的操作,直到数组完全排序\r\n\r\n具体按以下步骤实现:\r\n\r\n- 1,创建两个指针分别指向数组的最左端以及最右端\r\n- 2,在数组中任意取出一个元素作为基准\r\n- 3,左指针开始向右移动,遇到比基准大的停止\r\n- 4,右指针开始向左移动,遇到比基准小的元素停止,交换左右指针所指向的元素\r\n- 5,重复3,4,直到左指针超过右指针,此时,比基准小的值就都会放在基准的左边,比基准大的值会出现在基准的右边\r\n- 6,然后分别对基准的左右两边重复以上的操作,直到数组完全排序\r\n\r\n注意这里的基准该如何选择喃?最简单的一种做法是每次都是选择最左边的元素作为基准:\r\n\r\n\r\n\r\n但这对几乎已经有序的序列来说,并不是最好的选择,它将会导致算法的最坏表现。还有一种做法,就是选择中间的数或通过 `Math.random()` 来随机选取一个数作为基准,下面的代码实现就是以随机数作为基准。\r\n\r\n**代码实现**\r\n\r\n```js\r\nlet quickSort = (arr) =\u003e {\r\n quick(arr, 0 , arr.length - 1)\r\n}\r\n\r\nlet quick = (arr, left, right) =\u003e {\r\n let index\r\n if(left \u003c right) {\r\n // 划分数组\r\n index = partition(arr, left, right)\r\n if(left \u003c index - 1) {\r\n quick(arr, left, index - 1)\r\n }\r\n if(index \u003c right) {\r\n quick(arr, index, right)\r\n }\r\n }\r\n}\r\n\r\n// 一次快排\r\nlet partition = (arr, left, right) =\u003e {\r\n // 取中间项为基准\r\n var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],\r\n i = left,\r\n j = right\r\n // 开始调整\r\n while(i \u003c= j) {\r\n \r\n // 左指针右移\r\n while(arr[i] \u003c datum) {\r\n i++\r\n }\r\n \r\n // 右指针左移\r\n while(arr[j] \u003e datum) {\r\n j--\r\n }\r\n \r\n // 交换\r\n if(i \u003c= j) {\r\n swap(arr, i, j)\r\n i += 1\r\n j -= 1\r\n }\r\n }\r\n return i\r\n}\r\n\r\n// 交换\r\nlet swap = (arr, i , j) =\u003e {\r\n let temp = arr[i]\r\n arr[i] = arr[j]\r\n arr[j] = temp\r\n}\r\n\r\n// 测试\r\nlet arr = [1, 3, 2, 5, 4]\r\nquickSort(arr)\r\nconsole.log(arr) // [1, 2, 3, 4, 5]\r\n// 第 2 个最大值\r\nconsole.log(arr[arr.length - 2]) // 4\r\n```\r\n\r\n快排是从小到大排序,所以第 `k` 个最大值在 `n-k` 位置上\r\n\r\n**复杂度分析**\r\n\r\n- 时间复杂度:O(nlog~2~n)\r\n- 空间复杂度:O(nlog~2~n)\r\n\r\n## 14.5 希尔排序\r\n\r\n1959年Shell发明,第一个突破 O(n^2^) 的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。\r\n\r\n#### 插入排序\r\n\r\n插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入\r\n\r\n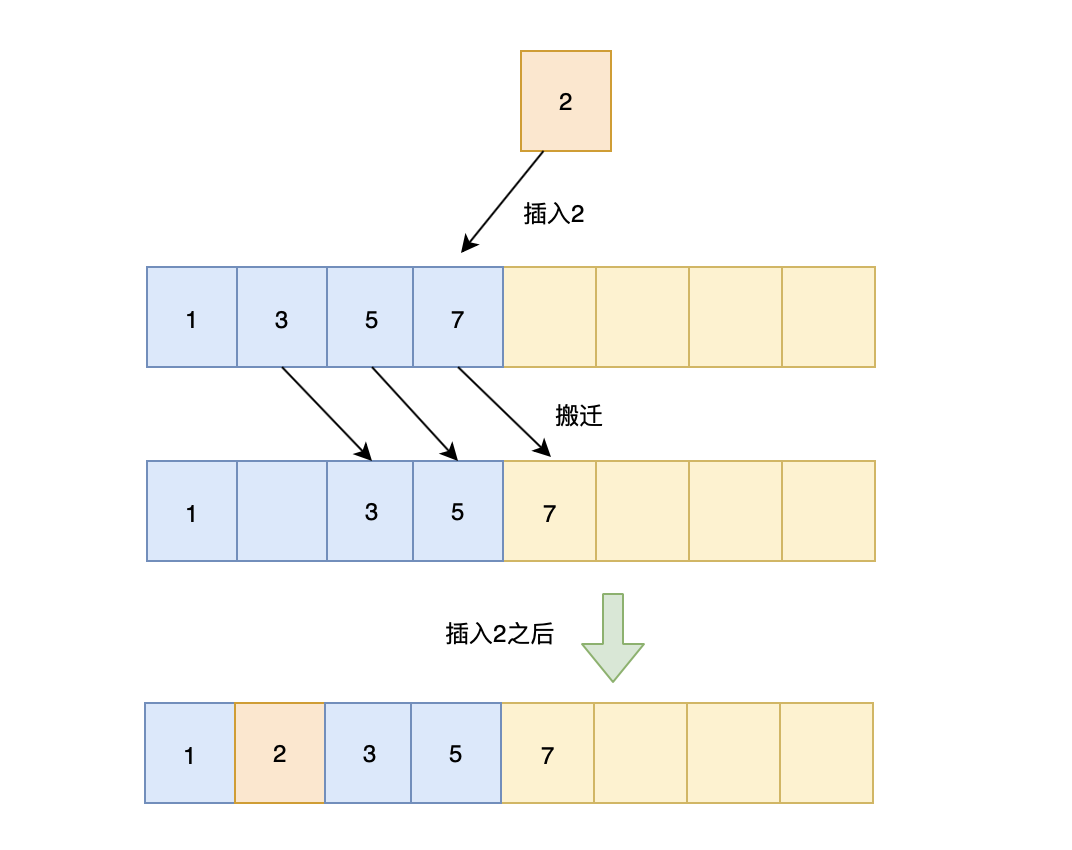\r\n\r\n**代码实现:**\r\n\r\n```js\r\nfunction insertionSort(arr) {\r\n let n = arr.length;\r\n let preIndex, current;\r\n for (let i = 1; i \u003c n; i++) {\r\n preIndex = i - 1;\r\n current = arr[i];\r\n while (preIndex \u003e= 0 \u0026\u0026 arr[preIndex] \u003e current) {\r\n arr[preIndex + 1] = arr[preIndex];\r\n preIndex--;\r\n }\r\n arr[preIndex + 1] = current;\r\n }\r\n return arr;\r\n}\r\n```\r\n\r\n插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。\r\n\r\n**复杂度分析:**\r\n\r\n- 时间复杂度:O(n^2^)\r\n- 空间复杂度:O(1)\r\n\r\n#### 希尔排序\r\n\r\n回顾一下上面的插入排序:\r\n\r\n- 第一趟插入排序后,我们得到的有效序列长度为 `2` \r\n- 第二趟插入排序后,我们得到的有效序列长度为 `3`\r\n- ...\r\n- 直到这个序列有序\r\n\r\n所以,如果序列足够乱的话,时间复杂度为 O(n^2^)\r\n\r\n希尔排序又是如何优化的喃?\r\n\r\n希尔排序又叫**缩小增量排序**,就是把数列进行分组(组内不停使用插入排序),直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换)。\r\n\r\n其中组的数量称为 **增量** ,显然的是,增量是不断递减的(直到增量为1)\r\n\r\n那我们有是如何进行分组喃?\r\n\r\n**往往的:**如果一个数列有 `8` 个元素,我们第一趟的增量是 `4` ,第二趟的增量是 `2` ,第三趟的增量是 `1` 。如果一个数列有 `18` 个元素,我们第一趟的增量是 `9` ,第二趟的增量是 `4` ,第三趟的增量是`2` ,第四趟的增量是 `1`\r\n\r\n很明显我们可以用一个序列来表示增量:`n/2、(n/2)/2、...、1`,**每次增量都**`/2`\r\n\r\n例如:\r\n\r\n```js\r\nlet arr = [4, 1, 5, 8, 7, 3]\r\n```\r\n\r\n**排序前:**\r\n\r\n- 将该数组看成三组( `Math.floor(arr.length/2)` ),分别是: `[4, 1]` , `[5, 8]` , `[7, 3]`\r\n\r\n**第一趟排序:**\r\n\r\n- 对三组数据分别进行插入排序,因此我们三个数组得到的结果为: `[1, 4]` , `[5, 8]` , `[3, 7]`\r\n\r\n此时数组是这样子的:`[1, 4, 5, 8, 3, 7]`\r\n\r\n**第二趟排序:**\r\n\r\n- 增量减少了,上面增量是 `3` ,此时增量应该为 `1` 了,因此把 `[1, 4, 5, 8, 3, 7]` 看成一个数组(**从宏观上是有序的了**),对其进行插入排序,**直至有序**\r\n\r\n**代码实现:**\r\n\r\n```js\r\nfunction shellSort(arr) {\r\n let n = arr.length;\r\n for (let gap = Math.floor(n / 2); gap \u003e 0; gap = Math.floor(gap / 2)) {\r\n for (let i = gap; i \u003c n; i++) {\r\n let j = i;\r\n let current = arr[i];\r\n while (j - gap \u003e= 0 \u0026\u0026 current \u003c arr[j - gap]) {\r\n arr[j] = arr[j - gap];\r\n j = j - gap;\r\n }\r\n arr[j] = current;\r\n }\r\n }\r\n return arr;\r\n}\r\n```\r\n\r\n**复杂度分析:**\r\n\r\n- 时间复杂度:O(nlogn)\r\n- 空间复杂度:O(1)\r\n\r\n## 14.6 计数排序\r\n\r\n**原理**\r\n\r\n计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。\r\n\r\n作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。它是一种典型的拿空间换时间的排序算法\r\n\r\n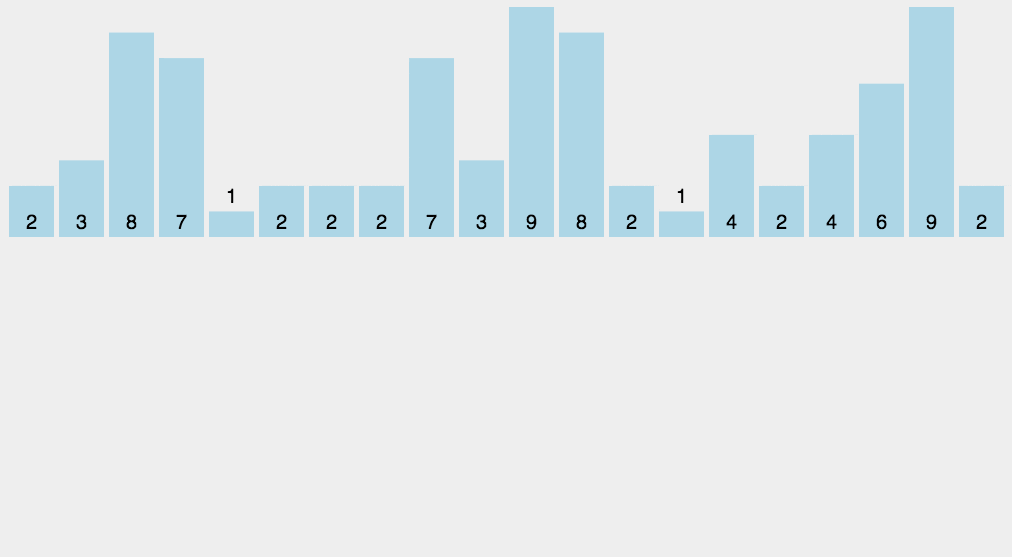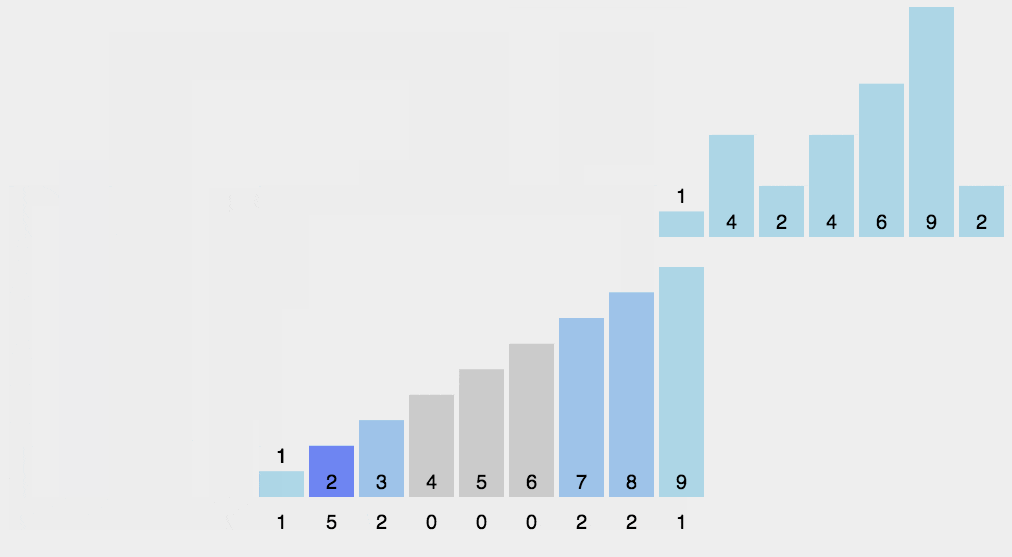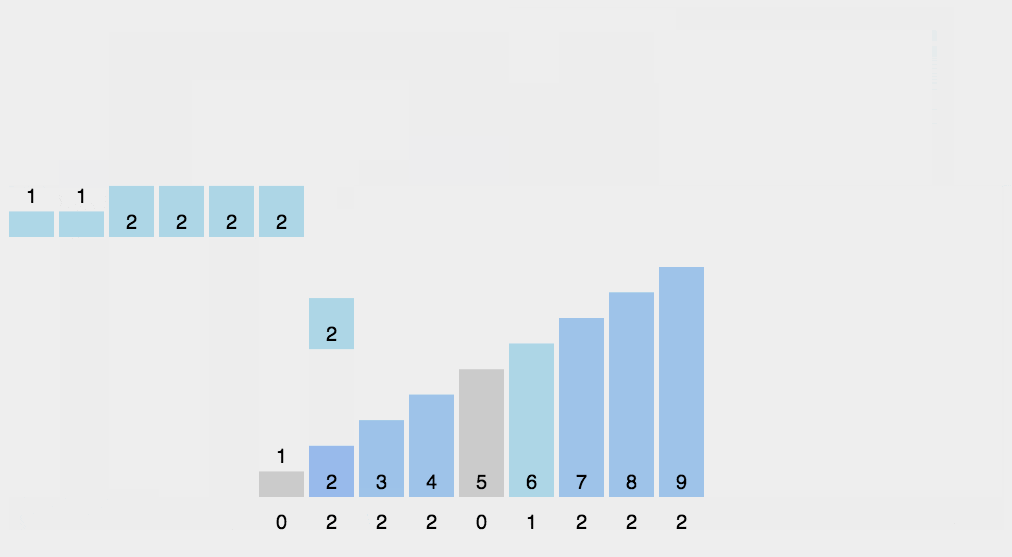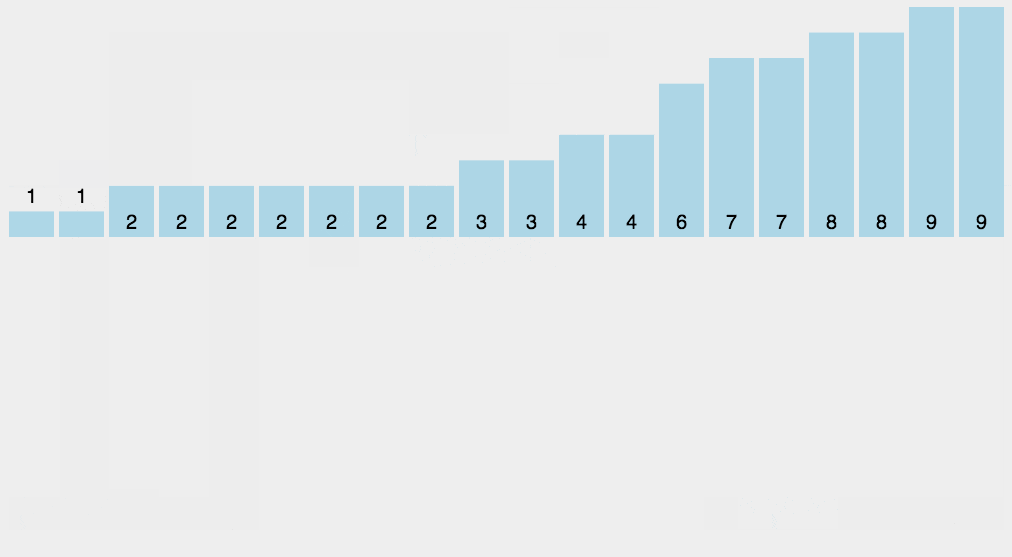\r\n\r\n**代码实现**\r\n\r\n```js\r\nfunction countingSort(arr, maxValue) =\u003e {\r\n // 开辟的新的数组,用于将输入的数据值转化为键存储\r\n var bucket = new Array(maxValue + 1),\r\n sortedIndex = 0,\r\n arrLen = arr.length,\r\n bucketLen = maxValue + 1\r\n\r\n // 存储\r\n for (var i = 0; i \u003c arrLen; i++) {\r\n if (!bucket[arr[i]]) {\r\n bucket[arr[i]] = 0\r\n }\r\n bucket[arr[i]]++\r\n }\r\n\r\n // 将数据从bucket按顺序写入arr中\r\n for (var j = 0; j \u003c bucketLen; j++) {\r\n while(bucket[j]-- \u003e 0) {\r\n arr[sortedIndex++] = j\r\n }\r\n }\r\n return arr\r\n}\r\n```\r\n\r\n**复杂度分析**\r\n\r\n- 时间复杂度:O(n+k)\r\n- 空间复杂度:O(n+k)\r\n\r\n## 14.7 桶排序\r\n\r\n**原理**\r\n\r\n桶排序是计数排序的升级版。它也是利用函数的映射关系。\r\n\r\n桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。\r\n\r\n完整步骤:\r\n\r\n- 首先使用 arr 来存储频率\r\n- 然后创建一个数组(有数量的桶),将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标(桶内)即可。\r\n\r\n```js\r\n// 桶排序\r\nlet bucketSort = (arr) =\u003e {\r\n let bucket = [], res = []\r\n arr.forEach((value, key) =\u003e {\r\n // 利用映射关系(出现频率作为下标)将数据分配到各个桶中\r\n if(!bucket[value]) {\r\n bucket[value] = [key]\r\n } else {\r\n bucket[value].push(key)\r\n }\r\n })\r\n // 遍历获取出现频率\r\n for(let i = 0;i \u003c= bucket.length - 1;i++){\r\n if(bucket[i]) {\r\n res.push(...bucket[i])\r\n }\r\n\t}\r\n\treturn res\r\n}\r\n```\r\n\r\n**复杂度分析:**\r\n\r\n- 时间复杂度:O(n)\r\n- 空间复杂度:O(n)\r\n\r\n## 14.8 基数排序\r\n\r\n**原理**\r\n\r\n基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。\r\n\r\n完整步骤:\r\n\r\n- 取得数组中的最大数,并取得位数;\r\n- arr为原始数组,从最低位开始取每个位组成radix数组;\r\n- 对radix进行计数排序(利用计数排序适用于小范围数的特点);\r\n\r\n**动图演示**\r\n\r\n\r\n\r\n**代码实现**\r\n\r\n```js\r\n//LSD Radix Sort\r\nvar counter = [];\r\nfunction radixSort(arr, maxDigit) {\r\n var mod = 10;\r\n var dev = 1;\r\n for (var i = 0; i \u003c maxDigit; i++, dev *= 10, mod *= 10) {\r\n for(var j = 0; j \u003c arr.length; j++) {\r\n var bucket = parseInt((arr[j] % mod) / dev);\r\n if(counter[bucket]==null) {\r\n counter[bucket] = [];\r\n }\r\n counter[bucket].push(arr[j]);\r\n }\r\n var pos = 0;\r\n for(var j = 0; j \u003c counter.length; j++) {\r\n var value = null;\r\n if(counter[j]!=null) {\r\n while ((value = counter[j].shift()) != null) {\r\n arr[pos++] = value;\r\n }\r\n }\r\n }\r\n }\r\n return arr;\r\n}\r\n```\r\n\r\n**复杂度分析**\r\n\r\n- 时间复杂度:基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的\r\n- 空间复杂度:O(n+k),其中k为桶的数量。一般来说n\u003e\u003ek,因此额外空间需要大概n个左右\r\n\r\n\r\n\r\n#### 基数排序 vs 计数排序 vs 桶排序\r\n\r\n这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:\r\n\r\n- 基数排序:根据键值的每位数字来分配桶;\r\n- 计数排序:每个桶只存储单一键值;\r\n- 桶排序:每个桶存储一定范围的数值;\r\n\r\n\r\n\r\n## 14.9 堆排序\r\n\r\n**原理**\r\n\r\n堆是一棵完全二叉树,它可以使用数组存储,并且大顶堆的最大值存储在根节点(i=1),所以我们可以每次取大顶堆的根结点与堆的最后一个节点交换,此时最大值放入了有效序列的最后一位,并且有效序列减1,有效堆依然保持完全二叉树的结构,然后堆化,成为新的大顶堆,重复此操作,知道有效堆的长度为 0,排序完成。\r\n\r\n完整步骤为:\r\n\r\n- 将原序列(n个)转化成一个大顶堆\r\n- 设置堆的有效序列长度为 n\r\n- 将堆顶元素(第一个有效序列)与最后一个子元素(最后一个有效序列)交换,并有效序列长度减1\r\n- 堆化有效序列,使有效序列重新称为一个大顶堆\r\n- 重复以上2步,直到有效序列的长度为 1,排序完成\r\n\r\n**动图演示**\r\n\r\n\r\n\r\n**代码实现**\r\n\r\n```js\r\nfunction heapSort(items) {\r\n // 构建大顶堆\r\n buildHeap(items, items.length-1)\r\n // 设置堆的初始有效序列长度为 items.length - 1\r\n let heapSize = items.length - 1\r\n for (var i = items.length - 1; i \u003e 1; i--) {\r\n // 交换堆顶元素与最后一个有效子元素\r\n swap(items, 1, i);\r\n // 有效序列长度减 1\r\n heapSize --;\r\n // 堆化有效序列(有效序列长度为 currentHeapSize,抛除了最后一个元素)\r\n heapify(items, heapSize, 1);\r\n }\r\n return items;\r\n}\r\n\r\n// 原地建堆\r\n// items: 原始序列\r\n// heapSize: 有效序列长度\r\nfunction buildHeap(items, heapSize) {\r\n // 从最后一个非叶子节点开始,自上而下式堆化\r\n for (let i = Math.floor(heapSize/2); i \u003e= 1; --i) { \r\n heapify(items, heapSize, i); \r\n }\r\n}\r\nfunction heapify(items, heapSize, i) {\r\n // 自上而下式堆化\r\n while (true) {\r\n var maxIndex = i;\r\n if(2*i \u003c= heapSize \u0026\u0026 items[i] \u003c items[i*2] ) {\r\n maxIndex = i*2;\r\n }\r\n if(2*i+1 \u003c= heapSize \u0026\u0026 items[maxIndex] \u003c items[i*2+1] ) {\r\n maxIndex = i*2+1;\r\n }\r\n if (maxIndex === i) break;\r\n swap(items, i, maxIndex); // 交换 \r\n i = maxIndex; \r\n }\r\n} \r\nfunction swap(items, i, j) {\r\n let temp = items[i]\r\n items[i] = items[j]\r\n items[j] = temp\r\n}\r\n\r\n// 测试\r\nvar items = [,1, 9, 2, 8, 3, 7, 4, 6, 5]\r\nheapSort(items)\r\n// [empty, 1, 2, 3, 4, 5, 6, 7, 8, 9]\r\n```\r\n\r\n测试成功\r\n\r\n**复杂度分析**\r\n\r\n- **时间复杂度:**建堆过程的时间复杂度是 `O(n)` ,排序过程的时间复杂度是 `O(nlogn)` ,整体时间复杂度是 `O(nlogn)`\r\n- **空间复杂度:** `O(1)`\r\n","author":{"url":"https://github.com/sisterAn","@type":"Person","name":"sisterAn"},"datePublished":"2021-04-16T14:10:54.000Z","interactionStatistic":{"@type":"InteractionCounter","interactionType":"https://schema.org/CommentAction","userInteractionCount":1},"url":"https://github.com/165/JavaScript-Algorithms/issues/165"}| route-pattern | /_view_fragments/issues/show/:user_id/:repository/:id/issue_layout(.:format) |
| route-controller | voltron_issues_fragments |
| route-action | issue_layout |
| fetch-nonce | v2:1fcc762d-f7e6-a4e0-85ab-235c0b938f2a |
| current-catalog-service-hash | 81bb79d38c15960b92d99bca9288a9108c7a47b18f2423d0f6438c5b7bcd2114 |
| request-id | E874:1FA820:DD3899:135FBEF:69725C93 |
| html-safe-nonce | 2e67da3fcf978dbd7dd476f6195837c080f89b7893d3376f4ba560a793b47f33 |
| visitor-payload | eyJyZWZlcnJlciI6IiIsInJlcXVlc3RfaWQiOiJFODc0OjFGQTgyMDpERDM4OTk6MTM1RkJFRjo2OTcyNUM5MyIsInZpc2l0b3JfaWQiOiI3OTE1MTA4Njc1MDkxNTg2MTk1IiwicmVnaW9uX2VkZ2UiOiJpYWQiLCJyZWdpb25fcmVuZGVyIjoiaWFkIn0= |
| visitor-hmac | 2a11a3f087bd4c60b88373732963becf7a9b1b5236792d2f927a4d915f6981a2 |
| hovercard-subject-tag | issue:859852139 |
| github-keyboard-shortcuts | repository,issues,copilot |
| google-site-verification | Apib7-x98H0j5cPqHWwSMm6dNU4GmODRoqxLiDzdx9I |
| octolytics-url | https://collector.github.com/github/collect |
| analytics-location | / |
| fb:app_id | 1401488693436528 |
| apple-itunes-app | app-id=1477376905, app-argument=https://github.com/_view_fragments/issues/show/sisterAn/JavaScript-Algorithms/165/issue_layout |
| twitter:image | https://opengraph.githubassets.com/689dc8e2b217f980494610c5fc5088de3be6a7439e8f88dd5f64ef14616179cf/sisterAn/JavaScript-Algorithms/issues/165 |
| twitter:card | summary_large_image |
| og:image | https://opengraph.githubassets.com/689dc8e2b217f980494610c5fc5088de3be6a7439e8f88dd5f64ef14616179cf/sisterAn/JavaScript-Algorithms/issues/165 |
| og:image:alt | 14.1 冒泡排序 原理: 从左到右,相邻元素进行比较,如果前一个元素值大于后一个元素值(正序),则交换,这样一轮下来,将最大的数在最右边冒泡出来。这样一轮一轮下来,最后实现从小到大排序。 动图演示: 代码实现: function bubbleSort(arr) { for (let i = 0; i < arr.length; i++) { for (let j = 0; j < arr.... |
| og:image:width | 1200 |
| og:image:height | 600 |
| og:site_name | GitHub |
| og:type | object |
| og:author:username | sisterAn |
| hostname | github.com |
| expected-hostname | github.com |
| None | f5a890431069e39e7eb98c8c81da83629b10b51afe674db42bf829dbc0abba43 |
| turbo-cache-control | no-preview |
| go-import | github.com/sisterAn/JavaScript-Algorithms git https://github.com/sisterAn/JavaScript-Algorithms.git |
| octolytics-dimension-user_id | 19721451 |
| octolytics-dimension-user_login | sisterAn |
| octolytics-dimension-repository_id | 252061924 |
| octolytics-dimension-repository_nwo | sisterAn/JavaScript-Algorithms |
| octolytics-dimension-repository_public | true |
| octolytics-dimension-repository_is_fork | false |
| octolytics-dimension-repository_network_root_id | 252061924 |
| octolytics-dimension-repository_network_root_nwo | sisterAn/JavaScript-Algorithms |
| turbo-body-classes | logged-out env-production page-responsive |
| disable-turbo | false |
| browser-stats-url | https://api.github.com/_private/browser/stats |
| browser-errors-url | https://api.github.com/_private/browser/errors |
| release | 26c781f26acd529068611189d77d95c57099561a |
| ui-target | full |
| theme-color | #1e2327 |
| color-scheme | light dark |
Links:
Viewport: width=device-width