Title: 腾讯&字节&阿里:介绍一下快排原理以及时间复杂度,并实现一个快排 · Issue #70 · sisterAn/JavaScript-Algorithms · GitHub
Open Graph Title: 腾讯&字节&阿里:介绍一下快排原理以及时间复杂度,并实现一个快排 · Issue #70 · sisterAn/JavaScript-Algorithms
X Title: 腾讯&字节&阿里:介绍一下快排原理以及时间复杂度,并实现一个快排 · Issue #70 · sisterAn/JavaScript-Algorithms
Description: 快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。 快排的过程简单的说只有三步: 首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition) 然后分别对基准的左右两边重复以上的操作,直到数组完全排序 具体按以下步骤实现: 1,创建两个指...
Open Graph Description: 快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。 快排的过程简单的说只有三步: 首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition) 然后分别对基准...
X Description: 快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。 快排的过程简单的说只有三步: 首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition) 然后分别对基准...
Opengraph URL: https://github.com/sisterAn/JavaScript-Algorithms/issues/70
X: @github
Domain: github.com
{"@context":"https://schema.org","@type":"DiscussionForumPosting","headline":"腾讯\u0026字节\u0026阿里:介绍一下快排原理以及时间复杂度,并实现一个快排","articleBody":"快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。\r\n\r\n快排的过程简单的说只有三步:\r\n\r\n- 首先从序列中选取一个数作为基准数\r\n- 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 `partition`)\r\n- 然后分别对基准的左右两边重复以上的操作,直到数组完全排序\r\n\r\n具体按以下步骤实现:\r\n\r\n- 1,创建两个指针分别指向数组的最左端以及最右端\r\n- 2,在数组中任意取出一个元素作为基准\r\n- 3,左指针开始向右移动,遇到比基准大的停止\r\n- 4,右指针开始向左移动,遇到比基准小的元素停止,交换左右指针所指向的元素\r\n- 5,重复3,4,直到左指针超过右指针,此时,比基准小的值就都会放在基准的左边,比基准大的值会出现在基准的右边\r\n- 6,然后分别对基准的左右两边重复以上的操作,直到数组完全排序\r\n\r\n注意这里的基准该如何选择喃?最简单的一种做法是每次都是选择最左边的元素作为基准:\r\n\r\n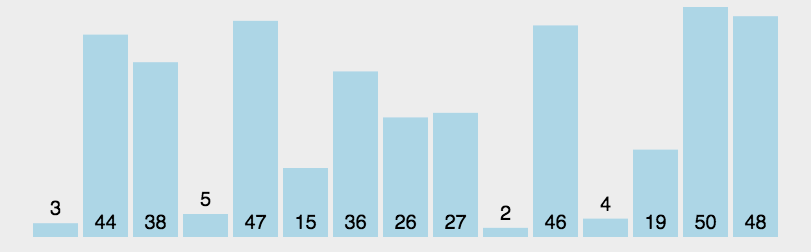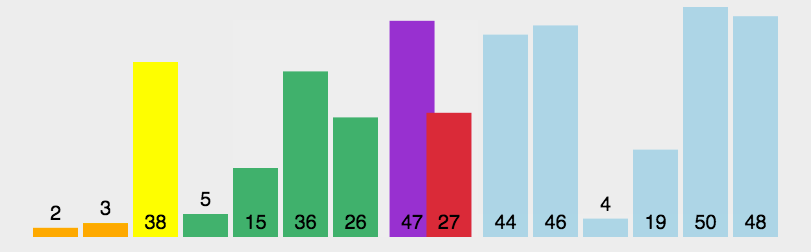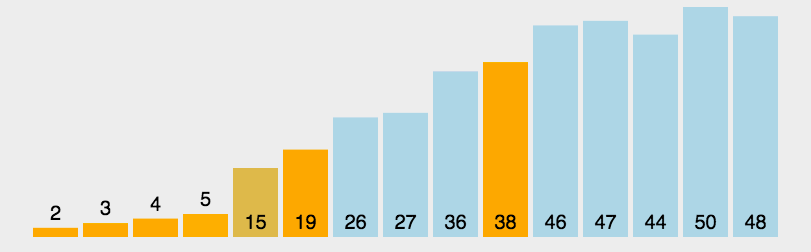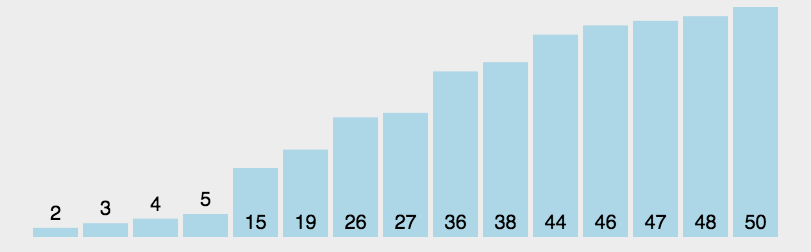\r\n\r\n但这对几乎已经有序的序列来说,并不是最好的选择,它将会导致算法的最坏表现。还有一种做法,就是选择中间的数或通过 `Math.random()` 来随机选取一个数作为基准,下面的代码实现就是以随机数作为基准。\r\n\r\n**代码实现**\r\n\r\n```js\r\nlet quickSort = (arr) =\u003e {\r\n quick(arr, 0 , arr.length - 1)\r\n}\r\n\r\nlet quick = (arr, left, right) =\u003e {\r\n let index\r\n if(left \u003c right) {\r\n // 划分数组\r\n index = partition(arr, left, right)\r\n if(left \u003c index - 1) {\r\n quick(arr, left, index - 1)\r\n }\r\n if(index \u003c right) {\r\n quick(arr, index, right)\r\n }\r\n }\r\n}\r\n\r\n// 一次快排\r\nlet partition = (arr, left, right) =\u003e {\r\n // 取中间项为基准\r\n var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],\r\n i = left,\r\n j = right\r\n // 开始调整\r\n while(i \u003c= j) {\r\n \r\n // 左指针右移\r\n while(arr[i] \u003c datum) {\r\n i++\r\n }\r\n \r\n // 右指针左移\r\n while(arr[j] \u003e datum) {\r\n j--\r\n }\r\n \r\n // 交换\r\n if(i \u003c= j) {\r\n swap(arr, i, j)\r\n i += 1\r\n j -= 1\r\n }\r\n }\r\n return i\r\n}\r\n\r\n// 交换\r\nlet swap = (arr, i , j) =\u003e {\r\n let temp = arr[i]\r\n arr[i] = arr[j]\r\n arr[j] = temp\r\n}\r\n\r\n// 测试\r\nlet arr = [1, 3, 2, 5, 4]\r\nquickSort(arr)\r\nconsole.log(arr) // [1, 2, 3, 4, 5]\r\n// 第 2 个最大值\r\nconsole.log(arr[arr.length - 2]) // 4\r\n```\r\n\r\n快排是从小到大排序,所以第 `k` 个最大值在 `n-k` 位置上\r\n\r\n**复杂度分析**\r\n\r\n- 时间复杂度:O(nlogn)\r\n- 空间复杂度:O(nlogn)","author":{"url":"https://github.com/sisterAn","@type":"Person","name":"sisterAn"},"datePublished":"2020-06-23T15:44:10.000Z","interactionStatistic":{"@type":"InteractionCounter","interactionType":"https://schema.org/CommentAction","userInteractionCount":7},"url":"https://github.com/70/JavaScript-Algorithms/issues/70"}| route-pattern | /_view_fragments/issues/show/:user_id/:repository/:id/issue_layout(.:format) |
| route-controller | voltron_issues_fragments |
| route-action | issue_layout |
| fetch-nonce | v2:d5cb582a-86f8-44e3-f2c3-89339f37c919 |
| current-catalog-service-hash | 81bb79d38c15960b92d99bca9288a9108c7a47b18f2423d0f6438c5b7bcd2114 |
| request-id | 8CDC:2265AE:13A1FEE:1B0B877:696AA035 |
| html-safe-nonce | 3f19f3f571b2d73a91c7de91f701faf5df6fb2135cb152d653e243f11b9ac2b9 |
| visitor-payload | eyJyZWZlcnJlciI6IiIsInJlcXVlc3RfaWQiOiI4Q0RDOjIyNjVBRToxM0ExRkVFOjFCMEI4Nzc6Njk2QUEwMzUiLCJ2aXNpdG9yX2lkIjoiNzE5NzQ1MjM0MTgxMDQ3MDk2NSIsInJlZ2lvbl9lZGdlIjoiaWFkIiwicmVnaW9uX3JlbmRlciI6ImlhZCJ9 |
| visitor-hmac | 86ebcfdf78acec4b97034db0be943f18546b72af94d365a78dfdd41a5ae505da |
| hovercard-subject-tag | issue:643949611 |
| github-keyboard-shortcuts | repository,issues,copilot |
| google-site-verification | Apib7-x98H0j5cPqHWwSMm6dNU4GmODRoqxLiDzdx9I |
| octolytics-url | https://collector.github.com/github/collect |
| analytics-location | / |
| fb:app_id | 1401488693436528 |
| apple-itunes-app | app-id=1477376905, app-argument=https://github.com/_view_fragments/issues/show/sisterAn/JavaScript-Algorithms/70/issue_layout |
| twitter:image | https://opengraph.githubassets.com/7280a6729460bd01837493e2df92db831c1249f10107e3c2ddaf84f3a8666154/sisterAn/JavaScript-Algorithms/issues/70 |
| twitter:card | summary_large_image |
| og:image | https://opengraph.githubassets.com/7280a6729460bd01837493e2df92db831c1249f10107e3c2ddaf84f3a8666154/sisterAn/JavaScript-Algorithms/issues/70 |
| og:image:alt | 快排使用了分治策略的思想,所谓分治,顾名思义,就是分而治之,将一个复杂的问题,分成两个或多个相似的子问题,在把子问题分成更小的子问题,直到更小的子问题可以简单求解,求解子问题,则原问题的解则为子问题解的合并。 快排的过程简单的说只有三步: 首先从序列中选取一个数作为基准数 将比这个数大的数全部放到它的右边,把小于或者等于它的数全部放到它的左边 (一次快排 partition) 然后分别对基准... |
| og:image:width | 1200 |
| og:image:height | 600 |
| og:site_name | GitHub |
| og:type | object |
| og:author:username | sisterAn |
| hostname | github.com |
| expected-hostname | github.com |
| None | a51f97dbb9326f71c08ecb61577457d543c602124d1a2672871258ef37ac5261 |
| turbo-cache-control | no-preview |
| go-import | github.com/sisterAn/JavaScript-Algorithms git https://github.com/sisterAn/JavaScript-Algorithms.git |
| octolytics-dimension-user_id | 19721451 |
| octolytics-dimension-user_login | sisterAn |
| octolytics-dimension-repository_id | 252061924 |
| octolytics-dimension-repository_nwo | sisterAn/JavaScript-Algorithms |
| octolytics-dimension-repository_public | true |
| octolytics-dimension-repository_is_fork | false |
| octolytics-dimension-repository_network_root_id | 252061924 |
| octolytics-dimension-repository_network_root_nwo | sisterAn/JavaScript-Algorithms |
| turbo-body-classes | logged-out env-production page-responsive |
| disable-turbo | false |
| browser-stats-url | https://api.github.com/_private/browser/stats |
| browser-errors-url | https://api.github.com/_private/browser/errors |
| release | 4bd0eac606c70914085176ef312ebdcd97a8cdf1 |
| ui-target | canary-1 |
| theme-color | #1e2327 |
| color-scheme | light dark |
Links:
Viewport: width=device-width