Title: 贪心算法套路问题 · Issue #171 · sisterAn/JavaScript-Algorithms · GitHub
Open Graph Title: 贪心算法套路问题 · Issue #171 · sisterAn/JavaScript-Algorithms
X Title: 贪心算法套路问题 · Issue #171 · sisterAn/JavaScript-Algorithms
Description: 最近在不间断、碎片的看贪心算法问题,相比回溯、动态规划问题,贪心算法理论最简单,死扣理论解决问题却很难,大部分的贪心问题一眼懵,很难看出是贪心问题,也很难找到解题套路,因此此部分介绍几道典型的贪心问题,并总结一套贪心套路帮助解题 贪心算法 算法策略 贪心算法,故名思义,总是做出当前的最优选择,即期望通过局部的最优选择获得整体的最优选择。 某种意义上说,贪心算法是很贪婪、很目光短浅的,它不从整体考虑,仅仅只关注当前的最大利益,所以说它做出的选择仅仅是某种意义上的局部最优,...
Open Graph Description: 最近在不间断、碎片的看贪心算法问题,相比回溯、动态规划问题,贪心算法理论最简单,死扣理论解决问题却很难,大部分的贪心问题一眼懵,很难看出是贪心问题,也很难找到解题套路,因此此部分介绍几道典型的贪心问题,并总结一套贪心套路帮助解题 贪心算法 算法策略 贪心算法,故名思义,总是做出当前的最优选择,即期望通过局部的最优选择获得整体的最优选择。 某种意义上说,贪心算法是很贪婪、很目光短浅的,它不从整...
X Description: 最近在不间断、碎片的看贪心算法问题,相比回溯、动态规划问题,贪心算法理论最简单,死扣理论解决问题却很难,大部分的贪心问题一眼懵,很难看出是贪心问题,也很难找到解题套路,因此此部分介绍几道典型的贪心问题,并总结一套贪心套路帮助解题 贪心算法 算法策略 贪心算法,故名思义,总是做出当前的最优选择,即期望通过局部的最优选择获得整体的最优选择。 某种意义上说,贪心算法是很贪婪、很目光短浅的,它不从整...
Opengraph URL: https://github.com/sisterAn/JavaScript-Algorithms/issues/171
X: @github
Domain: github.com
{"@context":"https://schema.org","@type":"DiscussionForumPosting","headline":"贪心算法套路问题","articleBody":"最近在不间断、碎片的看贪心算法问题,相比回溯、动态规划问题,贪心算法理论最简单,死扣理论解决问题却很难,大部分的贪心问题一眼懵,很难看出是贪心问题,也很难找到解题套路,因此此部分介绍几道典型的贪心问题,并总结一套贪心套路帮助解题\r\n\r\n## 贪心算法\r\n\r\n#### 算法策略\r\n\r\n贪心算法,故名思义,总是做出当前的最优选择,即期望通过局部的最优选择获得整体的最优选择。\r\n\r\n某种意义上说,贪心算法是很贪婪、很目光短浅的,它不从整体考虑,仅仅只关注当前的最大利益,所以说它做出的选择仅仅是某种意义上的局部最优,但是贪心算法在很多问题上还是能够拿到最优解或较优解,所以它的存在还是有意义的。\r\n\r\n在日常生活中,我们使用到贪心算法的时候还是挺多的,例如:从100章面值不等的钞票中,抽出 10 张,怎样才能获得最多的价值?\r\n\r\n我们只需要每次都选择剩下的钞票中最大的面值,最后一定拿到的就是最优解,这就是使用的贪心算法,并且最后得到了整体最优解。\r\n\r\n往往遇到的问题并不是这么简单,例如:\r\n\r\n#### 二倍数对数组问题\r\n\r\n给定一个长度为偶数的整数数组 `arr`,只有对 `arr` 进行重组后可以满足\r\n\r\n- 对于每个 `0 \u003c= i \u003c len(arr) / 2` ,都有 `arr[2 * i + 1] = 2 * arr[2 * i]` 时,返回 `true`;\r\n- 否则,返回 `false`。\r\n\r\n例如:\r\n\r\n```javascript\r\n输入:arr = [4,-2,2,-4]\r\n输出:true\r\n解释:可以用 [-2,-4] 和 [2,4] 这两组组成 [-2,-4,2,4] 或是 [2,4,-2,-4]\r\n```\r\n\r\n**解题思路:**\r\n\r\n`[4,-2,2,-4]` ,假设正数正向排序、负数逆向排序,得到 `[-2,-4,2,4]` ,那么遍历数组,每个数要不被之前的数匹配,要不之后存在 `2` 倍数\r\n\r\n- 例如对于 `arr[0]=-2` 只能存在 `2` 倍数,不会存在 `1/2` 的数\r\n\r\n也就是从 `arr[0]` 开始,仅仅只关注当前的 `2`倍数结果 ,仅仅关注当前局部的最优,通过每一步的最优解,获取全局最优解,这样看就是 **贪心算法** 问题\r\n\r\n以上这样思路,称之为 **抽象贪心算法模型**\r\n\r\n大部分的贪心问题,都很难看出来,我们最重要的是学会如何抽象成贪心算法模型,这步处理好,代码实现很简单\r\n\r\n对于本题,我们还需要关注重复数的问题,例如 `[2,2,4,4]` ,可以使用 `Set` 去重,`Map` 记录重复个数,实现如下:\r\n\r\n```javascript\r\nvar canReorderDoubled = function(arr) {\r\n if(arr.length \u003c 2) return false\r\n // 正数正序,负数逆序\r\n arr.sort((a, b)=\u003e{\r\n if(a\u003c0 \u0026\u0026 b\u003c0) return b-a\r\n return a-b\r\n })\r\n // 去重\r\n let nums = [...new Set(arr)], map = new Map()\r\n // 记录重复数个数\r\n for(let a of arr) {\r\n map.set(a, (map.get(a) || 0)+1)\r\n }\r\n \r\n for(let i=0; i\u003cnums.length; i++) {\r\n // 当前数与二倍数差值\r\n let temp = (map.get(nums[i] * 2) || 0)-map.get(nums[i])\r\n if(temp\u003e=0) { // 满足当前二倍数,或已匹配\r\n map.set(nums[i] * 2, temp) // 只关注当前最优,局部最优\r\n } else {\r\n // 不满足\r\n return false\r\n }\r\n }\r\n return true\r\n};\r\n```\r\n\r\n再看一道:\r\n\r\n#### 盛最多水的容器\r\n\r\n给定一个长度为 `n` 的整数数组 `height` 。有 `n` 条垂线,第 `i` 条线的两个端点是 ` (i, 0)` 和 `(i, height[i])` 。\r\n\r\n找出其中的两条线,使得它们与 `x` 轴共同构成的容器可以容纳最多的水。\r\n\r\n返回容器可以储存的最大水量。\r\n\r\n说明:你不能倾斜容器。\r\n\r\n\r\n\r\n示例:\r\n\r\n```javascript\r\n输入:[1,8,6,2,5,4,8,3,7]\r\n输出:49 \r\n解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。\r\n```\r\n\r\n**解题思路:**\r\n\r\n首先,两个边构成一个容器,这个容器的容水量由最短边和 `x` 轴间距决定,如果从 `x` 轴最大,即 `i=0, j=height.length-1` 开始选择两个边:\r\n\r\n- 如果我们选择两个边的最长边,向内收缩一步,长边可能变得更长,但储水量只由短边和 `x` 轴间距决定,短边不变,`x` 轴间距缩小了,储水量只可能缩小\r\n- 如果我们选择两个边的最短边,向内收缩一步,短边可能更长或缩小,如果更长的话,储水量可能会增加\r\n\r\n因此,我们只要选择每次的局部最优:短边向内收缩一步,使用 `res` 更新每次操作后的全局最优,最终拿到整体最优,这就是 **贪心算法** 问题\r\n\r\n以上这样思路,称之为 **抽象贪心算法模型**\r\n\r\n代码实现:\r\n\r\n```javascript\r\nvar maxArea = function(height) {\r\n if(height.length \u003c2) return 0\r\n let res = 0,\r\n i = 0,\r\n j = height.length-1\r\n while(i\u003cj) {\r\n res = Math.max(Math.min(height[j],height[i])*(j-i), res)\r\n // 收缩\r\n if(height[i]\u003cheight[j]) {\r\n i++\r\n } else {\r\n j--\r\n }\r\n }\r\n return res\r\n};\r\n```\r\n\r\n采用的是双指针解题,贪心算法是实现,双指针是实现手段,像回溯、动态规划都是思想,DFS、BFS是手段,所有的问题都离不开算法思想\r\n\r\n相似的有:[有效三角形的个数问题](https://leetcode-cn.com/problems/valid-triangle-number/solution/by-user7746o-aur9/)\r\n\r\n\r\n## 贪心套路\r\n\r\n#### 第一步 判定是否是贪心问题\r\n\r\n问题给出一组数据,并给出该组数据的条件或环境(限制),以及结果期望,要求判断这组数据是否满足期望,或从这组数据中选择部分数据,能否达到期望结果最优值\r\n\r\n例如:\r\n\r\n- 二倍数对数组问题:给出一组数据,限制数据重组后二倍数,判断所有的数据是否都满足二倍数关系\r\n- 盛最多水的容器问题:给出一组数据 `height` ,限制每两个数都可以构成容器,求从这组数据中选择两个数据,达到容器最大值\r\n\r\n#### 第二步 抽象贪心算法模型\r\n\r\n根据问题,抽象出符合满足局部最优,且能通过局部的最优选择获得整体的最优选择的贪心算法模型,例如:\r\n\r\n- 二倍数对数组问题:数据正数正向排序、负数逆向排序后,每个数都向后满足二倍数关系,则整体都满足二倍数关系\r\n- 盛最多水的容器问题:从 `i=0, j=height.length-1` 开始选择两个边,每次做出当前的最优选择:每次短边向内收缩一步,更新全局最优,最终拿到整体最优:容器最大值\r\n\r\n贪心算法模型是对当前问题的一种抽象,一种变体,帮助我们解决问题, **不要问如何抽象贪心算法模型,多刷几道,刷着刷着就有感觉了**\r\n\r\n#### 第三步 判断贪心解题是否最优\r\n\r\n通过示例判断结果是否是最优解\r\n\r\n## 经典案例:跳跃游戏\r\n\r\n给定一个非负整数数组 `nums` ,你最初位于数组的 **第一个下标** 。\r\n\r\n数组中的每个元素代表你在该位置可以跳跃的 **最大长度** 。\r\n\r\n判断你是否能够到达最后一个下标。\r\n\r\n示例:\r\n\r\n```javascript\r\n输入:nums = [2,3,1,1,4]\r\n输出:true\r\n解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标\r\n```\r\n\r\n**第一步 判定是否是贪心问题**\r\n\r\n给出一组数,限制每个数组代表能跳跃的最大长度,期待能够能够到达最后一个数字位置,贪心算法问题\r\n\r\n**第二步 抽象贪心算法模型**\r\n\r\n从下标 `i=0` 开始,选择当前局部最优,能够达到的最远位置 `i+nums[i]` ,然后和全局最优 `end` 对比,更新全局最优,最后拿到整体最优解\r\n\r\n```js\r\nvar canJump = function(nums) {\r\n // 全局最优\r\n let end = 0\r\n for(let i=0; i\u003cnums.length; i++) {\r\n // 当前位置不可达,超出此前所有最大可达位置\r\n if(end \u003c i) return false\r\n // 最大可达位置已经到达甚至超越最后一个下标,返回 true\r\n if(end \u003e= nums.length-1) return true\r\n // 更新全局最优\r\n end = end \u003e i+nums[i] ? end: i+nums[i]\r\n }\r\n return true\r\n};\r\n```\r\n\r\n**第三步 判断贪心解题是否最优**\r\n\r\n结合示例 `[2,3,1,1,4]` 验证结果正确\r\n\r\n```js\r\ncanJump([2,3,1,1,4]) // true\r\n```\r\n\r\n\r\n\r\n## 经典案例:跳跃游戏||\r\n\r\n给你一个非负整数数组 `nums` ,你最初位于数组的第一个位置。\r\n\r\n数组中的每个元素代表你在该位置可以跳跃的最大长度。\r\n\r\n你的目标是使用最少的跳跃次数到达数组的最后一个位置。\r\n\r\n假设你总是可以到达数组的最后一个位置。\r\n\r\n示例:\r\n\r\n```javascript\r\n输入: nums = [2,3,1,1,4]\r\n输出: 2\r\n解释: 跳到最后一个位置的最小跳跃数是 2。\r\n 从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。\r\n```\r\n\r\n**第一步 判定是否是贪心问题**\r\n\r\n给出一组数,限制每个数组代表能跳跃的最大长度,期待从中选择几个数字,能够最快(最少跳跃)到达最后一个数字位置,贪心算法问题\r\n\r\n**第二步 抽象贪心算法模型**\r\n\r\n从下标 `i=0` 开始,选择当前局部最优,能够达到的最远位置 `end=i+nums[i]` ,那么 `i+1、...、end` 为下一步跳跃可能的起点\r\n\r\n从 `i=i+1` 继续遍历,选择当前局部最优,能够达到的最远位置 `i+nums[i]` ,然后和全局最远 `maxPos` 对比,更新全局最远,直到 `i=end` ,当前步起点跳跃结束,开启下一步,上一步全局最远 `end` 和全局最远 `maxPos` 对比,更新全局最远 `end`\r\n\r\n这里 `end` 与 `maxPos` 不同:\r\n\r\n- `end` 为上一步全局最优,上一步跳跃所能达到的最远位置,也是这一步起跳点的最远位置\r\n- `maxPos` 为实时的全局最优,当启动新一轮跳跃时,为新一轮跳跃所能达到的最远位置\r\n\r\n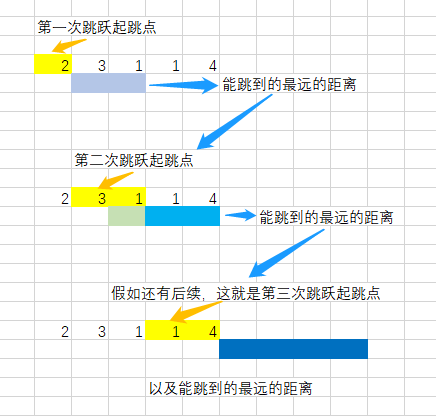\r\n\r\n图片来自:https://leetcode-cn.com/problems/jump-game-ii/solution/45-by-ikaruga/\r\n\r\n通过 `end` 选择每一轮的局部最优,更新跳跃次数,获取整体最优\r\n\r\n```js\r\nvar jump = function(nums) {\r\n let end = 0, \r\n maxPos = 0,\r\n count = 0\r\n for(let i=0; i\u003cnums.length-1; i++) {\r\n maxPos = maxPos \u003e i+nums[i] ? maxPos : i+nums[i]\r\n // 到达 count 轮终点,更新 end 与 count\r\n if(i === end) {\r\n // 启动下一轮\r\n end = maxPos\r\n // 更新跳跃次数\r\n count++\r\n }\r\n }\r\n return count\r\n}\r\n```\r\n\r\n**第三步 判断贪心解题是否最优**\r\n\r\n结合示例 `[2,3,1,1,4]` 验证结果正确\r\n\r\n```js\r\njump([2,3,1,1,4]) // 2\r\n```\r\n\r\n\r\n\r\n\r\n\r\n\r\n","author":{"url":"https://github.com/sisterAn","@type":"Person","name":"sisterAn"},"datePublished":"2022-04-10T13:57:30.000Z","interactionStatistic":{"@type":"InteractionCounter","interactionType":"https://schema.org/CommentAction","userInteractionCount":0},"url":"https://github.com/171/JavaScript-Algorithms/issues/171"}| route-pattern | /_view_fragments/issues/show/:user_id/:repository/:id/issue_layout(.:format) |
| route-controller | voltron_issues_fragments |
| route-action | issue_layout |
| fetch-nonce | v2:890d7ed4-a3e1-db20-da08-bbbc4fc32b1e |
| current-catalog-service-hash | 81bb79d38c15960b92d99bca9288a9108c7a47b18f2423d0f6438c5b7bcd2114 |
| request-id | 9E2A:323DD4:1382DB0:1AE9DCB:696AA06A |
| html-safe-nonce | 95035ed3afb5a6d6251e9e98b92a876ce79ee8722122c46fc55ad6c3c2cdc131 |
| visitor-payload | eyJyZWZlcnJlciI6IiIsInJlcXVlc3RfaWQiOiI5RTJBOjMyM0RENDoxMzgyREIwOjFBRTlEQ0I6Njk2QUEwNkEiLCJ2aXNpdG9yX2lkIjoiMzc5MzUzNjY1NjMwMzg5MDUzOCIsInJlZ2lvbl9lZGdlIjoiaWFkIiwicmVnaW9uX3JlbmRlciI6ImlhZCJ9 |
| visitor-hmac | 286464c56b4780900663bc5b0a16d56365a814b7151009371100c9dffe4f7629 |
| hovercard-subject-tag | issue:1199043640 |
| github-keyboard-shortcuts | repository,issues,copilot |
| google-site-verification | Apib7-x98H0j5cPqHWwSMm6dNU4GmODRoqxLiDzdx9I |
| octolytics-url | https://collector.github.com/github/collect |
| analytics-location | / |
| fb:app_id | 1401488693436528 |
| apple-itunes-app | app-id=1477376905, app-argument=https://github.com/_view_fragments/issues/show/sisterAn/JavaScript-Algorithms/171/issue_layout |
| twitter:image | https://opengraph.githubassets.com/50cfd94035ed45c6704f4d3def29b09430aeceab36f0bad649eac18afccca644/sisterAn/JavaScript-Algorithms/issues/171 |
| twitter:card | summary_large_image |
| og:image | https://opengraph.githubassets.com/50cfd94035ed45c6704f4d3def29b09430aeceab36f0bad649eac18afccca644/sisterAn/JavaScript-Algorithms/issues/171 |
| og:image:alt | 最近在不间断、碎片的看贪心算法问题,相比回溯、动态规划问题,贪心算法理论最简单,死扣理论解决问题却很难,大部分的贪心问题一眼懵,很难看出是贪心问题,也很难找到解题套路,因此此部分介绍几道典型的贪心问题,并总结一套贪心套路帮助解题 贪心算法 算法策略 贪心算法,故名思义,总是做出当前的最优选择,即期望通过局部的最优选择获得整体的最优选择。 某种意义上说,贪心算法是很贪婪、很目光短浅的,它不从整... |
| og:image:width | 1200 |
| og:image:height | 600 |
| og:site_name | GitHub |
| og:type | object |
| og:author:username | sisterAn |
| hostname | github.com |
| expected-hostname | github.com |
| None | a51f97dbb9326f71c08ecb61577457d543c602124d1a2672871258ef37ac5261 |
| turbo-cache-control | no-preview |
| go-import | github.com/sisterAn/JavaScript-Algorithms git https://github.com/sisterAn/JavaScript-Algorithms.git |
| octolytics-dimension-user_id | 19721451 |
| octolytics-dimension-user_login | sisterAn |
| octolytics-dimension-repository_id | 252061924 |
| octolytics-dimension-repository_nwo | sisterAn/JavaScript-Algorithms |
| octolytics-dimension-repository_public | true |
| octolytics-dimension-repository_is_fork | false |
| octolytics-dimension-repository_network_root_id | 252061924 |
| octolytics-dimension-repository_network_root_nwo | sisterAn/JavaScript-Algorithms |
| turbo-body-classes | logged-out env-production page-responsive |
| disable-turbo | false |
| browser-stats-url | https://api.github.com/_private/browser/stats |
| browser-errors-url | https://api.github.com/_private/browser/errors |
| release | 4bd0eac606c70914085176ef312ebdcd97a8cdf1 |
| ui-target | full |
| theme-color | #1e2327 |
| color-scheme | light dark |
Links:
Viewport: width=device-width