René's URL Explorer Experiment

{"@context":"https://schema.org","@type":"DiscussionForumPosting","headline":"一文详解RNN及股票预测实战(Python)","articleBody":"循环神经网络（RNN）是基于序列数据（如语言、语音、时间序列）的递归性质而设计的，是一种反馈类型的神经网络，其结构包含环和自重复，因此被称为“循环”。它专门用于处理序列数据，如逐字生成文本或预测时间序列数据(例如股票价格)。\r\n\r\n\r\n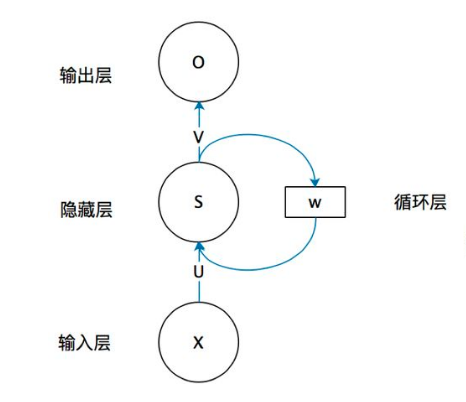![](https://img-blog.csdnimg.cn/img_convert/dce61188cad550ef7b9fa799a9092a65.png)\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n## 一、 RNN 网络类型\r\n\r\nRNN以输入数m对应输出数n的不同，可以划分为5种基础结构类型：\r\n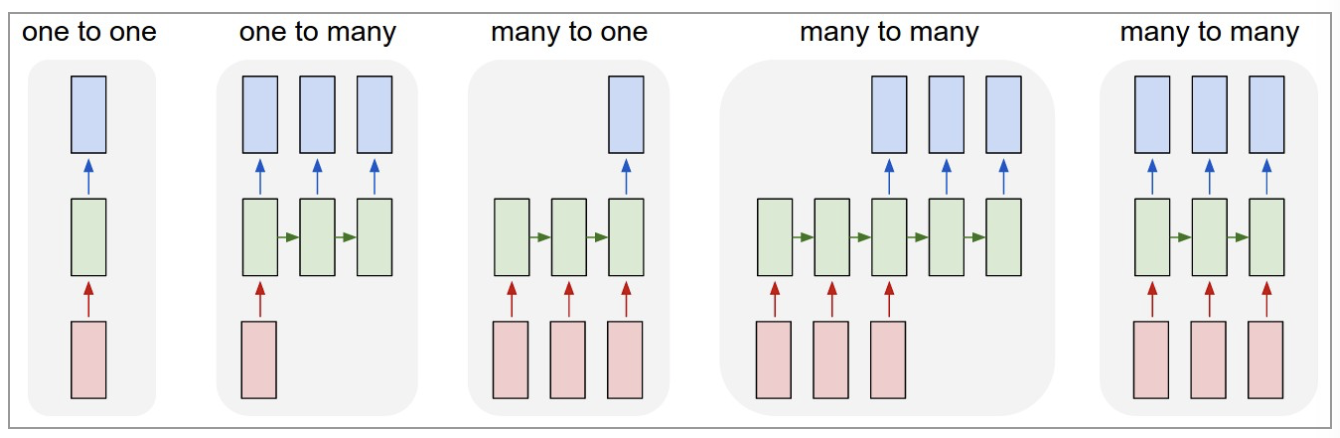![](https://img-blog.csdnimg.cn/img_convert/a4699bf7333d7cd62340c8d823d009a3.png)\r\n\r\n（1）one to one：其实和全连接神经网络并没有什么区别，这一类别算不上 RNN。\r\n\r\n（2）one to many：输入不是序列，输出是序列。可用于按主题生成文章或音乐等。\r\n\r\n（3）many to one：输入是序列，输出不是序列（为单个值）。常用于文本分类。\r\n\r\n（4）many to many：输入和输出都是不定长的序列。这也就是Encoder-Decoder结构，常用于机器翻译。\r\n\r\n（5）many to many(m==n)：输入和输出都是等长的序列数据。这是 RNN 中最经典的结构类型，常用于NLP的命名实体识别、序列预测，本文以此为例具体展开。\r\n\r\n## 二、RNN原理\r\n关于RNN模型，我们还是从数据、模型、学习目标、优化算法这几个要素展开解析，使用过程需要重点关注的是其输入和输出的差异（本节以经典的m==n的RNN结构为例）：\r\n### 2.1 数据层面\r\n\r\n不像传统的机器学习模型假设输入是独立的，RNN的输入数据元素有顺序及相互依赖的，并按时间步逐一的串行输入模型的。上一步的输入对下一步的预测是有影响的（如文字预测的任务，以“猫吃鱼”这段序列文字，上一步的输入“猫”--x(0)会影响下一步的预测“吃”--x(1)的概率，也会继续影响下下步的预测“鱼”--x(2)的概率），我们通过RNN结构就可以将历史的（上下文）的信息反馈到下一步。\r\n\r\n\r\n\r\n### 2.2 模型层面及前向传播\r\n\r\n![](https://img-blog.csdnimg.cn/img_convert/707ac25d5bb2f75f13a52dd51a53c91b.png)\r\n如上图，**RNN模型(如左侧模型，实际上也只有这一个物理模型)，按各个时间步展开后（如右侧模型），可以看作是按时间步(t)串联并共享($ U、W、V$ )参数的多个全连接神经网络**。展开后的立体图如下：\r\n![](https://img-blog.csdnimg.cn/img_convert/83d811d585d608fbc7eba7f5994a7ad7.png)\r\n\r\nRNN除了接受每一步的输入x(t)，同时还会连接输入上一步的反馈信息——隐藏状态h(t-1)，也就是当前时刻的隐藏状态 ℎ(t) 由当前时刻的输入 x(t)和上一时刻的隐藏状态h(t-1)共同决定。另外的，RNN神经元在每个时间步上是共享权重参数矩阵的（不同于CNN是空间上的参数共享），时间维度上的参数共享可以充分利用数据之间的时域关联性，如果我们在每个时间点都有一个单独的参数，不但不能泛化到训练时没有见过序列长度，也不能在时间上共享不同序列长度和不同位置的统计强度。\r\n\r\n如下**各时间步的前向传播计算流程图**，接下来我们会对计算流程逐步分解：\r\n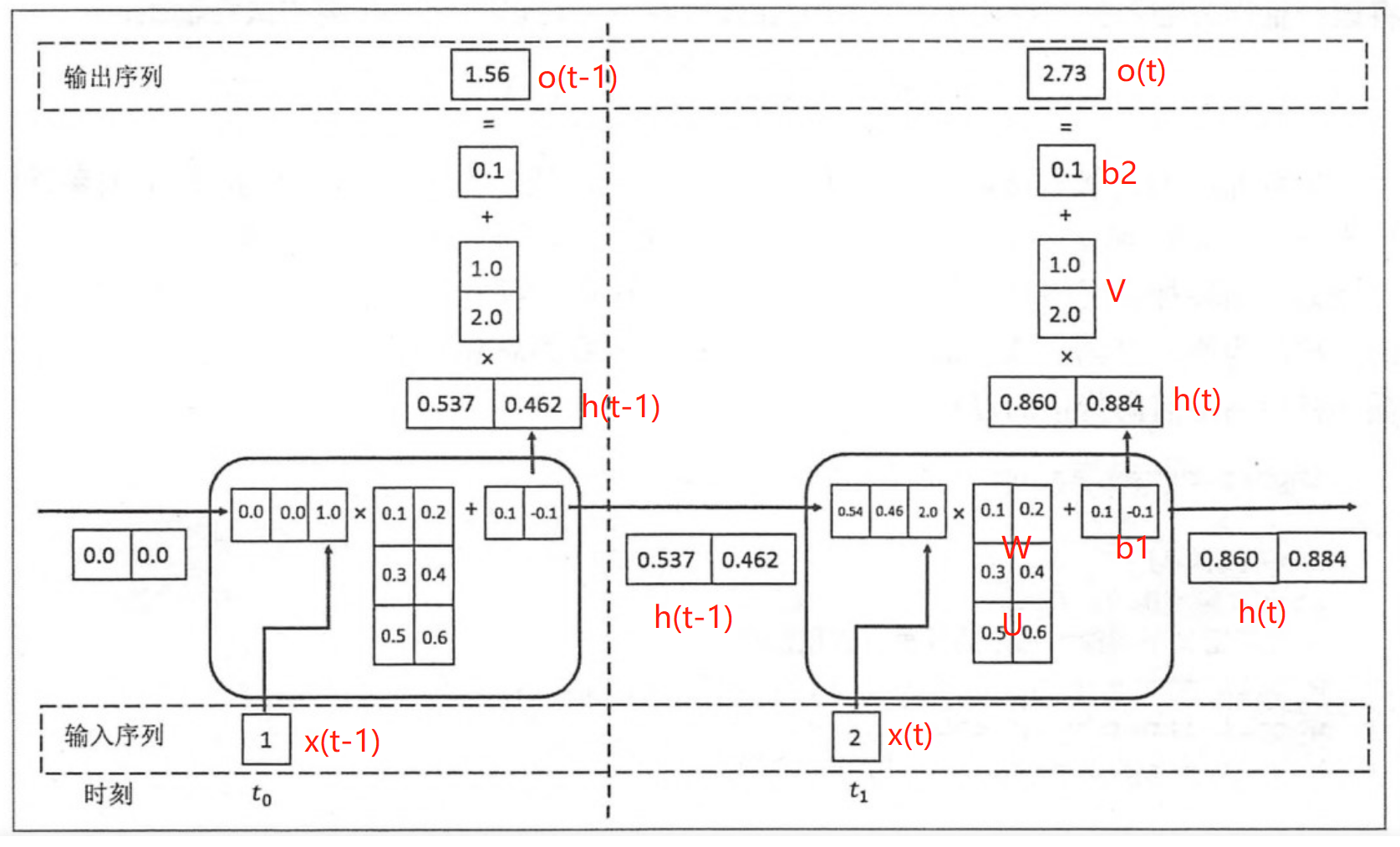![](https://img-blog.csdnimg.cn/img_convert/dea09563258d47c4bb6241ecba5006be.png)\r\n\u003e 上图展开了两个时间步t-1、t的计算过程；\r\nt取值为0~序列的长度m；\r\nx(t)是t时间步的 输入向量；\r\nU是 输入层到隐藏层的权重矩阵;\r\nh(t)是t时间步 隐藏层的输出状态向量，能表征历史输入（上下文）的反馈信息；\r\nV是 隐藏层到输出层的权重矩阵；\r\nb是 偏置项；\r\no(t)是t时间步 输出层的输出向量；\r\n#### 2.2.1   *t* 时间步的输入过程\r\n\u003e假设各时间步的状态h的维度为2，h初始值为[0,0]，输入x和输出o维度为1。\r\n\r\n将上一时刻的状态h(t-1)，与当前时刻的输入x(t)拼接成一维向量作为全连接的隐藏层的输入，对应隐藏层的的输入维度为3 （如下图的输入部分）。\r\n![](https://img-blog.csdnimg.cn/img_convert/8907cdca519123acf7d0f772bcb7b8cf.png)\r\n#### 2.2.2 *t*时间步输出h(t) 并反馈到下一步的过程\r\n对应到计算流程图上，t-1时刻输出的状态h(t-1)为[0.537, 0.462]，t时刻的输入为[2.0]，拼接之后为[0.537, 0.462, 2.0]输入全连接的隐藏层，隐藏层的权重矩阵$U+W$为[[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]]，偏置项b1为[0.1, -0.1]，经过隐藏层的矩阵运算为：h(t-1)拼接x(t) * 权重参数W 拼接 权重矩阵U + 偏置项(b1)再由tanh转换后输出为状态h(t)。接着h(t)与x(t+1)继续输入到下一步（t+1）的隐藏层。\r\n```python\r\n# 隐藏层的矩阵运算的对应代码\r\nnp.tanh(np.dot(np.array([[0.537, 0.462, 2.0]]),np.array([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]])) + np.array([0.1, -0.1]))\r\n# 输出h(t)为： array([[0.85972772, 0.88365397]])\r\n```\r\n#### 2.2.3 *t*时间步h(t) 到输出o(t)的过程\r\n\r\n隐藏层输出状态h(t)为[0.86, 0.884]，输出层权重矩阵$V$为[[1.0], [2.0]]，偏置项b1为[0.1], h(t)经由输出层的矩阵运算为：h(t) * V +偏置项(b2)后，输出o(t)\r\n```python\r\n# 输出层的矩阵运算的对应代码\r\nnp.dot(np.array([[0.85972772, 0.88365397]]),np.array([[1.0], [2.0]])) + np.array([0.1])\r\n# o(t) 输出: array([[2.72703566]])\r\n```\r\n上述过程从初始输入（t=0）遍历到序列结束(t=m)，就是一个完整的前向传播过程，我们可以看出权重矩阵$U、W、V$和偏置项在不同时刻都是同一组，这也说明RNN在不同时刻中是共享参数的。\r\n\r\n\r\n\r\n\r\n可以将这RNN计算过程简要概述为两个公式：\r\n\r\n\u003e状态h(t) = f( U * x(t) + W * h(t-1) + b1)，  f为激活函数，上图隐藏层用的是tanh。隐藏层激活函数常用tanh、relu\r\n\r\n\u003e输出o(t) = g( V * h(t) + b2)，g为激活函数，上图输出层做回归预测，没有用非线性激活函数。当用于分类任务，输出层一般用softmax激活函数\r\n\r\n\r\n### 2.3 学习目标\r\n\r\nRNN模型将输入 x(t)序列映射到输出值 o(t)后， 同全连接神经网络一样，可以衡量每个 o(t) 与相应的训练目标 y 的误差（如交叉熵、均方误差）作为损失函数，以最小化损失函数L(U,W,V)作为学习目标(也可以称为优化策略)。\r\n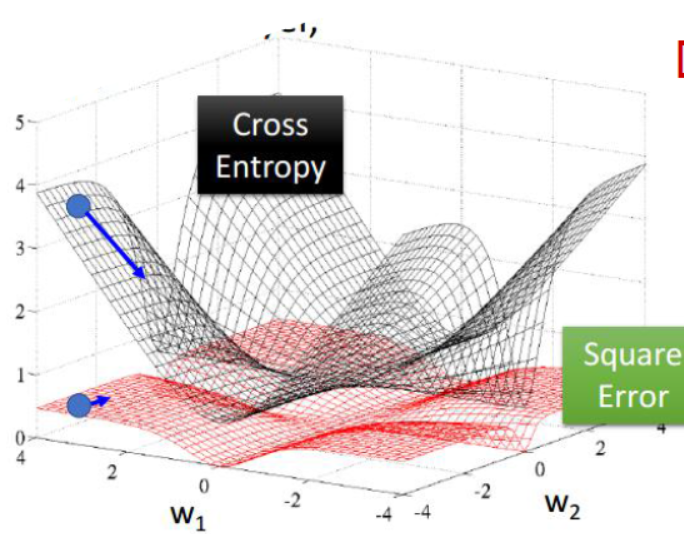![](https://img-blog.csdnimg.cn/img_convert/bba62d11e4fd86e93eb5ffaa0d5da986.png)\r\n\r\n\r\n### 2.4 优化算法\r\n\r\nRNN的优化过程与全连接神经网络没有本质区别，通过误差反向传播，多次迭代梯度下降优化参数，得到合适的RNN模型参数$ U,W,V$ （此处忽略偏置项） 。区别在于**RNN是基于时间反向传播**，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)，BPTT会对不同时间步的梯度求和，由于所有的参数在序列的各个位置是共享的，反向传播时我们更新的是相同的参数组。如下BPTT示意图及U,W,V求导（梯度）的过程。\r\n![](https://img-blog.csdnimg.cn/img_convert/7f4f22dc6702e5ea6a0166ae7d14d233.png)\r\n\r\n\r\n优化参数 $V$ 相对简单，求参数 $V$ 的偏导数，并对不同时间步的梯度求和：\r\n![](https://img-blog.csdnimg.cn/img_convert/97e7e253b8d89587944386dfdfd21cb6.png)\r\n$W$ 和 $U$ 的偏导的求解由于需要涉及到历史数据，其偏导求起来相对复杂，假设只有三个时刻(t==3)，那么在第三个时刻 $L$ 对 $W$ 的偏导数为：\r\n![](https://img-blog.csdnimg.cn/img_convert/b4a49916b57d547dad709398885eafbe.png)\r\n\r\n相应的，$L$ 在第三个时刻对U的偏导数为：\r\n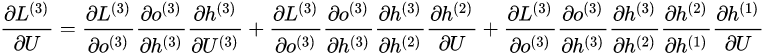![](https://img-blog.csdnimg.cn/img_convert/830bf4aa001eae53271a6ea10313d438.png)\r\n\r\n我们根据上面两个式子可以写出L在 $t$ 时刻对 $W$ 和 $U$ 偏导数的通式：\r\n![](https://img-blog.csdnimg.cn/img_convert/a4eeea57c03e01ef5450aef1f7157f17.png)\r\n\r\n- RNN优化的难点\r\n我们把激活函数（sigmoid、tanh）代入，分析上述通式的中间累乘的那部分：\r\n![](https://img-blog.csdnimg.cn/img_convert/67c0798d3cc55d014e04b49f2352ef0b.png)\r\nsigmoid函数的导数范围是(0,0.25]，tanh函数的导数范围是(0,1]。累乘的过程中，如果取sigmoid函数作为激活函数的话，随着时间步越长，较小导数累乘就会导致该时间步梯度越来越小直到接近于0（历史时间步的信息距离当前时间步越长，反馈的梯度信号就会越弱），这也就是“梯度消失”。同理，也可能会导致“梯度爆炸”。\r\n![](https://img-blog.csdnimg.cn/img_convert/e6dcf980bd628e15748ab4f629387295.png)\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n### 2.5 RNN的局限性\r\n\r\n- 上述展示的都是单向的 RNN，单向 RNN 有个缺点是在 t 时刻，无法使用 t+1 及之后时刻的序列信息，所以就有了双向循环神经网络（bidirectional RNN）。\r\n\r\n- 理论上RNN能够利用任意长序列的信息，但是实际中它能记忆的长度是有限的，经过一定的时间后将导致梯度爆炸或者梯度消失（如上节），即长期依赖（long-term dependencies）问题。一般的，使用传统RNN常需要对序列限定个最大长度、设定梯度截断以及引导信息流的正则化，或者使用门控RNN 如GRU、LSTM 以改善长期依赖问题（--后面专题讨论）。\r\n\r\n## 三、 RNN预测股票\r\n本项目通过创建单层隐藏层的RNN模型，输入前60个交易日（时间步）股票开盘价的时间序列数据，预测下一个（60+1）交易日的股票开盘价。\r\n![](https://img-blog.csdnimg.cn/img_convert/083d034dfe5fb8e0f7f1475bec2d189a.png)\r\n导入股票数据，选取股票开盘价的时间序列数据\r\n```python\r\nimport numpy as np\r\nimport matplotlib.pyplot as plt\r\nimport pandas as pd\r\n\r\n#（本公众号阅读原文访问数据集及源码）\r\ndataset_train = pd.read_csv('./data/NSE-TATAGLOBAL.csv')\r\ndataset_train = dataset_train.sort_values(by='Date').reset_index(drop=True)\r\ntraining_set = dataset_train.iloc[:, 1:2].values\r\nprint(dataset_train.shape)\r\ndataset_train.head()\r\n```\r\n\r\n\r\n对训练数据进行归一化，加速网络训练收敛。\r\n![](https://img-blog.csdnimg.cn/img_convert/2df061c87501b5de3282dabbabef9768.png)\r\n\r\n```python\r\n# 训练数据max-min归一化\r\nfrom sklearn.preprocessing import MinMaxScaler\r\nsc = MinMaxScaler(feature_range = (0, 1))\r\ntraining_set_scaled = sc.fit_transform(training_set)\r\n```\r\n将数据整理为样本及标签：60 timesteps and 1 output\r\n\r\n```python\r\n# 每条样本含60个时间步，对应下一时间步的标签值\r\nX_train = []\r\ny_train = []\r\nfor i in range(60, 2035):\r\n    X_train.append(training_set_scaled[i-60:i, 0])\r\n    y_train.append(training_set_scaled[i, 0])\r\nX_train, y_train = np.array(X_train), np.array(y_train)\r\n\r\nprint(X_train.shape)\r\nprint(y_train.shape)\r\n\r\n# Reshaping\r\nX_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))\r\nprint(X_train.shape)\r\n```\r\n利用kera创建单隐藏层的RNN模型，并设定模型优化算法adam， 目标函数均方根MSE\r\n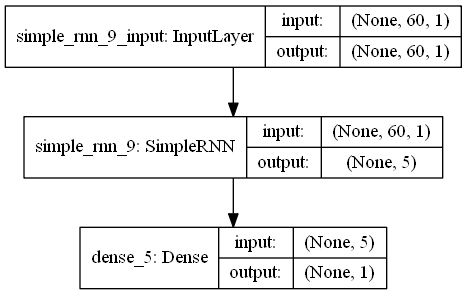![](https://img-blog.csdnimg.cn/img_convert/2f3771e26bc77195d69c039debe2bc95.png)\r\n\r\n```python\r\n#  利用Keras创建RNN模型\r\n\r\nfrom keras.models import Sequential\r\nfrom keras.layers import Dense\r\nfrom keras.layers import SimpleRNN,LSTM\r\nfrom keras.layers import Dropout\r\n\r\n\r\n# 初始化顺序模型\r\nregressor = Sequential()\r\n\r\n# 定义输入层及带5个神经元的隐藏层\r\nregressor.add(SimpleRNN(units = 5, input_shape = (X_train.shape[1], 1)))\r\n\r\n# 定义线性的输出层\r\nregressor.add(Dense(units = 1))\r\n\r\n# 模型编译：定义优化算法adam， 目标函数均方根MSE\r\nregressor.compile(optimizer = 'adam', loss = 'mean_squared_error')\r\n\r\n# 模型训练\r\nhistory = regressor.fit(X_train, y_train, epochs = 100, batch_size = 100, validation_split=0.1)\r\n\r\nregressor.summary()\r\n```\r\n展示模型拟合的情况：训练集、验证集均有较低的loss\r\n\r\n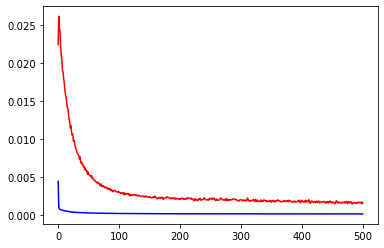![](https://img-blog.csdnimg.cn/img_convert/5943f2f2e9b0550abc49267b5c0da430.png)\r\n```\r\nplt.plot(history.history['loss'],c='blue')    # 蓝色线训练集损失\r\nplt.plot(history.history['val_loss'],c='red') # 红色线验证集损失\r\nplt.show()\r\n```\r\n\r\n评估模型：以新的时间段的股票交易系列数据作为测试集，评估模型测试集的表现。\r\n\r\n\r\n```python\r\n# 测试数据\r\ndataset_test = pd.read_csv('./data/tatatest.csv')\r\ndataset_test = dataset_test.sort_values(by='Date').reset_index(drop=True)\r\n\r\nreal_stock_price = dataset_test.iloc[:, 1:2].values\r\n\r\ndataset_total = pd.concat((dataset_train['Open'], dataset_test['Open']), axis = 0)\r\ninputs = dataset_total[len(dataset_total) - len(dataset_test) - 60:].values\r\ninputs = inputs.reshape(-1,1)\r\ninputs = sc.transform(inputs)\r\n\r\n# 提取测试集\r\nX_test = []\r\nfor i in range(60, 76):\r\n    X_test.append(inputs[i-60:i, 0])\r\nX_test = np.array(X_test)\r\nX_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))\r\n\r\n# 模型预测\r\npredicted_stock_price = regressor.predict(X_test)\r\n# 逆归一化\r\npredicted_stock_price = sc.inverse_transform(predicted_stock_price)\r\n# 模型评估\r\nprint('预测与实际差异MSE',sum(pow((predicted_stock_price - real_stock_price),2))/predicted_stock_price.shape[0])\r\nprint('预测与实际差异MAE',sum(abs(predicted_stock_price - real_stock_price))/predicted_stock_price.shape[0])\r\n```\r\n通过测试集评估，预测与实际差异MSE:53.03141531，预测与实际差异MAE ：5.82196445。可视化预测值与实际值的差异情况，预测对比实际值趋势有延后，但整体比较一致（注：本文仅从数据规律维度预测股价，仅供参考不构成任何投资建议，亏光了别找我！！！）。\r\n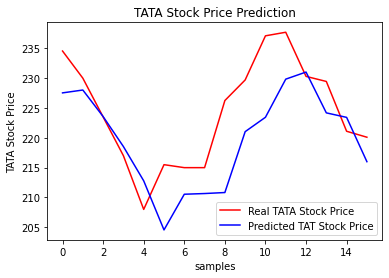![](https://img-blog.csdnimg.cn/img_convert/fc4d3c960e5d5ef6a4972ee0ba5e43cf.png)\r\n```python\r\n# 预测与实际差异的可视化\r\nplt.plot(real_stock_price, color = 'red', label = 'Real TATA Stock Price')\r\nplt.plot(predicted_stock_price, color = 'blue', label = 'Predicted TAT Stock Price')\r\nplt.title('TATA Stock Price Prediction')\r\nplt.xlabel('samples')\r\nplt.ylabel('TATA Stock Price')\r\nplt.legend()\r\nplt.show()\r\n```\r\n\r\n\r\n\r\n---\r\n文章首发于算法进阶，公众号阅读原文可访问[GitHub项目源码](https://github.com/aialgorithm/Blog)","author":{"url":"https://github.com/aialgorithm","@type":"Person","name":"aialgorithm"},"datePublished":"2021-12-01T13:08:12.000Z","interactionStatistic":{"@type":"InteractionCounter","interactionType":"https://schema.org/CommentAction","userInteractionCount":0},"url":"https://github.com/35/Blog/issues/35"}